Description of the project
The classical concept of positioning systems for a Global Navigation Satellite System (GNSS) would work ideally if all satellites and the receiver were at rest in an inertial reference frame. But at the level of precision needed by a GNSS, one has to consider curvature and relativistic inertial effects of spacetime, which are far from being negligible.
There are two very different ways of including relativity in a positioning system:
- keep the Newtonian conception of absolute time and space, and add a number of corrections depending on the desired accuracy, or
- use a relativistic positioning system.
The latter leads to numerous advantages, since it allows the definition of a very stable and accurate primary reference system, which could be used for many areas of science such as geology, gravitational wave detection or relativistic gravimetry.
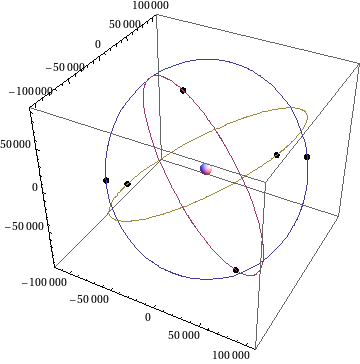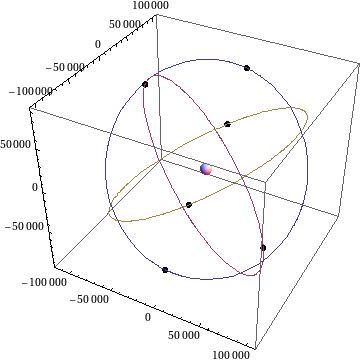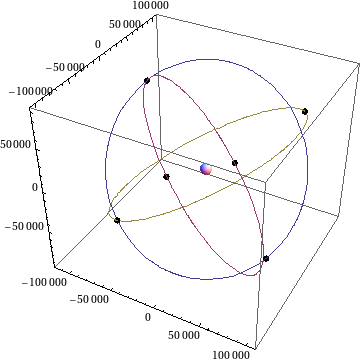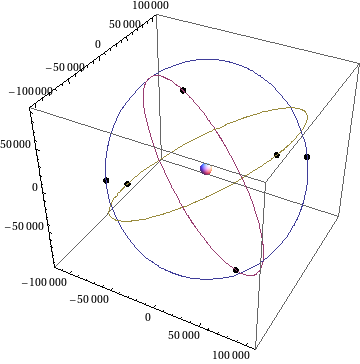
In order to research the concept of a relativistic GNSS, the European Space Agency (ESA) published in 2009 a Call for Proposals for the Ariadna study Mapping the Spacetime Metric with a Global Navigation Satellite System. The participants were prof. dr. Andrej Čadež and dr. Uroš Kostić from the Faculty of Mathematics and Physics, and Pacôme Delva from ESA. The aim of project was to answer the question, whether it is possible to "measure" the Earth with the future navigation system Galileo. Namely, the Galileo satellites will be able to communicate with each other, so it could be possible to determine by comparing measured and calculated times of flight of signals, if the metric around the Earth really is what we think it is.
We have shown that the use of fully relativistic code in GNSS systems offers an interesting alternative to using post-Newtonian approximations. The code, written and tested, executes a position finding algorithm in about 60~ms on a normal laptop computer if the initial position is completely unknown and a few times faster if the algorithm starts from a tighter dead reckoning position. This proves that the more consistent relativistic formalism presents no technical obstacle for use in modern global positioning devices.
Since new and interesting questions arose during this work, ESA decided to extend the project. On this occasion, we studied the relation between some preferred global coordinates and dynamically defined coordinates. We have shown that Autonomous Basis of Coordinates (ABC) can be precisely defined within a framework consisting of dynamical description of GNSS satellites and the description of light propagation between satellites. ABC can be extended in space via emission coordinates, if the dynamics of light propagation is known throughout the space. The dynamics of satellites of a GNSS constellation is well understood, since they move in the local gravitational field, dominated by that of the Earth, including contributions from the Moon, Sun and planets, while their mutual interaction may be neglected.
Successfully completed project on Galileo navigation system surely contributed to a successful application for the project Relativistic GNSS in the frame of PECS programme led by ESA. The project started on 1st of July 2011, with the following participants: Andreja Gomboc, Uroš Kostić, Martin Horvat, Pacôme Delva (SYRTE/Observatoire de Paris), and Sante Carloni (ESA/ESTEC). The aim of the project is to determine, to what level it is possible to improve the accuracy and stability of a global navigation system with respect to an Earth-fixed reference frame, where it is necessary to take into account also gravitational perturbations due to Moon, Sun, planets, Earth multi-poles, and Earth rotation when modelling motion of the satellites. Furthermore, we will also look into possibilities of scientific usage of such a system, e.g. for gravimetry and geology.
Briefly, by doing this kind of research, we look into possibilities and search for solutions to use general relativity in a global navigation system. Planned inter-satellite communication and a better definition of time can drastically improve the accuracy of GNSS and thus expand its applicability. The improved accuracy of all four coordinates will be in particular welcome in traffic, geodesy, and geodynamics. Furthermore, such a system would enable a better understanding of the shape, gravitational potential, rotation of Earth, and motion of tectonic plates. The expected substantial technological improvements of the GNSS will make the system a powerful new scientific tool which will have the potential to make significant scientific contributions.

